基于直接神经控制器的伺服控制系统设计
本章讲述了基本的神经网络控制器。提出了使用直接神经控制器是一种可在线调整线性组合中关键参数的在线神经网络。
摘要:传统意义上的PID控制器具有结构简单、调节方便、参数设置和工程索引密切相关的优势。但它也有一定的局限性:对复杂系统很难建立数学模型,当控制对象不同时,控制器的参数很难自动适应外部环境的变化,且很难对一些复杂的过程和参数进行有效控制。而神经网络控制的发展、应用和与PID控制的结合,在一定程度上解决了传统PID控制器难以进行在线实时参数自整定等方面的缺点,可以充分发挥PID控制的优点。本章讲述了基本的神经网络控制器。提出了使用直接神经控制器是一种可在线调整线性组合中关键参数的在线神经网络。
关键词:直接神经网络,伺服控制,神经协调器
DesigntoServoControlSystemBasedonDirectNeuralNetworksController
Mingxue.Cai
(QingDaoQingdaorubbermachineryresearchinstitute)
0前言
用来精确地跟随或复现某个过程的反馈控制系统。在很多情况下,伺服系统专指被控制量(系统的输出量)是机械位移或位移速度、加速度的反馈控制系统,其作用是使输出的机械位移(或转角)准确地跟踪输入的位移(或转角)。伺服系统的结构组成和其他形式的反馈控制系统没有原则上的区别。
伺服控制系统是一种能对试验装置的机械运动按预定要求进行自动控制的操作系统。在很多情况下,伺服系统专指被控制量(系统的输出量)是机械位移或位移速度、加速度的反馈控制系统,其作用是使输出的机械位移(或转角)准确地跟踪输入的位移(或转角)。伺服系统的结构组成和其他形式的反馈控制系统没有原则上的区别。
伺服驱动装置是机电一体化设备的重要组成部分。随着微电子技术的发展,交流伺服技术正朝着交流化、数字化、小型化的方向迅速发展。在伺服控制系统设计过程中,应充分考虑稳定和响应两项重要指标,而这些因素很多程度上取决于伺服驱动系统的特性。在传统的PID控制伺服系统过程中,稳定性和快速性无法同时满足。针对上述缺点,国内外学者积极探索采用人工智能控制的理论和方法。神经网络具有极强的非线性动态跟踪能力和自适应学习能力,对控制对象的数学模型无依赖性,在智能控制过程中得到广泛的应用。针对神经网络的以上特点,提出了基于神经网络的伺服系统控制方法,以神经网络为控制器,设计了基于神经网络的伺服控制系统。
1.直接神经控制器
一个三层的直接神经控制器。已知被控对象的定性知识或者被控对象的雅可比值,一个带有隐藏层的三层神经网络可以计算出输出值的任意判别边界。尽管有两个隐藏层的神经网络在一些专门问题上能获得更好的近似值,但也更容易陷入局部极小,需要更多的CPU时间。
此外,还将考虑一个隐藏曾里面包含的正确单元的数目。李普曼提供了全面的几何论据以及推理来证明为什么一个单隐藏层中单元的最大数目等于M(N+1),其中M是输出单元的数目,N为输入单元的数目。已经测试了一个传播跟踪控制系统上单隐含层的不同数目单元的数目。最终发现,一个带有三至五个隐藏层的网络足够给出一个满意的结果。
1.1直接神经控制器的算法本文提出的直接神经控制器是有两个输入单元,一个输出单元,若干隐含单元的三层神经网络。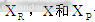 分别代表需要的命令输入,参考模型的输出和被控对象的输出。网络的两个输入是误差以及它关于
分别代表需要的命令输入,参考模型的输出和被控对象的输出。网络的两个输入是误差以及它关于 的微分。
的微分。
参考模型可以按照标准二阶传递函数设计,阻尼比和固有频率可以按照被控对象的物理特性定义。
直接控制器的算法和权值更新方程由下述方程表述。
这里的直接神经控制器有隐含层(下标j),输出层(下标k)和输入层(下标i).为了标准化为-1和+1,输入信号在输入层被乘以增益 。
。
。切线双曲函数作为隐含层和输出层的激活函数。隐含层的单元数目等于J。输入层的单元数目等于I。输出层的单元数目等于K。隐含层中j节点的输入为:

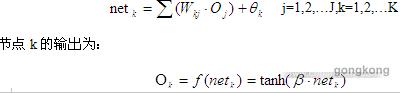

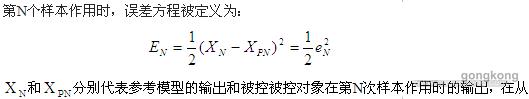
N次改变到N+1次的时间间隙,权值矩阵得到更新。

这里:

可以由公式以上两式得到。神经网络中的连接权在从样本N到样本N+1改变的过程中得到更新。

切线双曲函数作为激活函数,使得神经网络控制器输出
(19.4)是介于-1和+1之间的值,再乘以尺度因子
作为被控对象的输入。初始化置权值和偏值为+0.5到-0.5之间的最小随机数。根据以上两公式更新数值。
1.2在线调节的自适应神经控制器
根据前面公式已知,被控对象的雅克比值需要预先知道。然而,因为被控对象的动态特性,确切的
很难决定。用微分近似的方法,在很小的的范围内改变被控对象的每个输入,并测量输出的变化,雅克比是指:
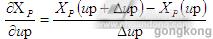
或者,将微分关系的变量的变化与之前迭代的值比较,微分可以由以下关系近似:
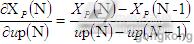
当被控制被控对象惯性大或者有干扰时,使用公式近似时经常造成模棱两可的情况。这种情况说明神经控制器在输入和输出之间建立了一种因果关系。这是与期望的情形相违背的。
一个简单的正负号函数,用来近似被控对象的雅克比值。被称为是工业跟踪控制应用的在线训练自适应神经控制器。因此,用 的变化率来近似
的变化率来近似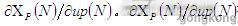 被他们的符号函数代替。因此根据公式:
被他们的符号函数代替。因此根据公式:
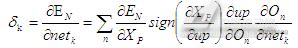
清楚地了解控制信号 可以提供需要的符号信息。因此,
可以提供需要的符号信息。因此,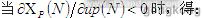
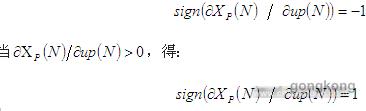
用以上公式得到的给定的微分的符号,神经控制器将根据被控对象的输出误差e(N),有效地输出正确方向的控制信号。
2神经协调器的权值更新
输出层和隐含层,隐含层和输入层之间的加权系数修正公式分别为:
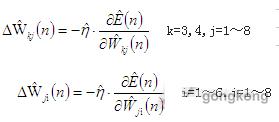
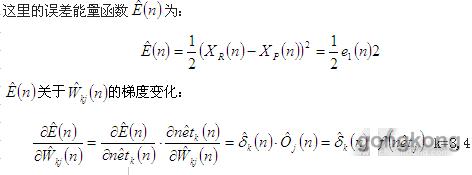

这里的
根据 可由误差和其微分的线性组合所近似,神经网络
可由误差和其微分的线性组合所近似,神经网络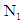 的输出层的第n-1次权值更新为:
的输出层的第n-1次权值更新为:


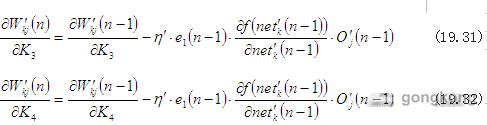
权值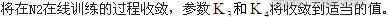
3.总结
传统的简单结构的直接神经控制器可以容易地执行,节省更多的CPU时间。但是被控对象的雅克比值不容易知道。传统的在线训练神经控制器使用正负号函数近似雅克比值还不足以用于伺服控制系统。δ适应法则可以有效提高收敛速率,但是合适的参数取决于尝试和误差,获得合适的参数不容易。这里提出的MNNACS可以为传统的直接神经控制(DNC)提供合适的参数。带有被MNNACS训练好参数的DNC可以提高自适应能力以及改善非线性控制系统的控制性能。
提交
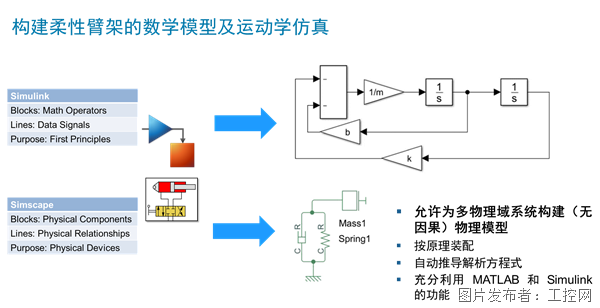
超越传统直觉,MATLAB/Simulink助力重型机械的智能化转型
新大陆自动识别精彩亮相2024华南国际工业博览会
派拓网络被Forrester评为XDR领域领导者
智能工控,存储强基 | 海康威视带来精彩主题演讲
展会|Lubeworks路博流体供料系统精彩亮相AMTS展会









 投诉建议
投诉建议