3D结构光相机技术原理分为时间编码和空间编码,上次讲过时间编码,今天就来讲讲空间编码——
空间编码
为满足动态场景的需要,可以采用空间编码结构光。前面谈到了随机结构光,就是不带编码信息,投影随机纹理,而这里讨论的空间编码结构光特指向被测空间中投影经过数学编码的、一定范围内的光斑不具备重复性的结构光。由此,某个点的编码值可以通过其临域获得。其中,包含一个完整的空间编码的像素数量(窗口大小)就决定了重建的精度。
·德布鲁因序列(De Bruijn)序列
德布鲁因序列(维基百科)B(k,)表示用k个符号(如二进制,k=2)来表示长度为的循环编码,为一个编码值的长度。
举例:最简单的,k=2时,采用二进制符号(0,1),编码值的长度n=2,可以得到一个长度为的循环序列:【0,0,1,1】。此时,我们得到4个长度为2的不同的编码:【0,0】,【0,1】,【1,1】,【1,0】.
因此,某种结构光就可以按照该德布鲁因序列进行编码。而获得的结构光影像中,以上4个像素的编码为【0,0,1,1】,通过一个大小为2的滑动窗口(假定一个结构光光斑或光束的宽度是一个像素)即可获取每个像素的编码值。同样地,如果是经过极线校正的双目图像,只需要搜索对应的行即可,此时只要求编码在轴上不具备重复性。此时的结构光就是竖直条带状的。
当然,为了提高编码效率,也可以使用灰度图、彩色图像等比0-1编码具有更多可能编码值的投影方式。例如,对于RGB影像,采用二进
制编码(即某种颜色只有有、无两种状态),则共有种颜色组合,去除(0,0,0),还剩下7种颜色。因此k=7,=3,这样就可以获得
一个长度为343的条带序列。对于这个序列,唯一的约束为:相邻的条带不能为同样的颜色。否则对于解码算法来说很容易造成误差。下图展示了只使用5种颜色(k=5,=3)的结构光序列:

二维空间编码
德布鲁因序列是一种一维编码,可以将之扩展到二维空间中,使得对于一个x*y大小的二维空间,其中一个w*大小的子窗口所包含的编码值在这整个二维编码序列中只出现一次。
如上面中的4*6的M-arrays序列中,每个2*2大小的窗口所包含的编码值都是唯一的。
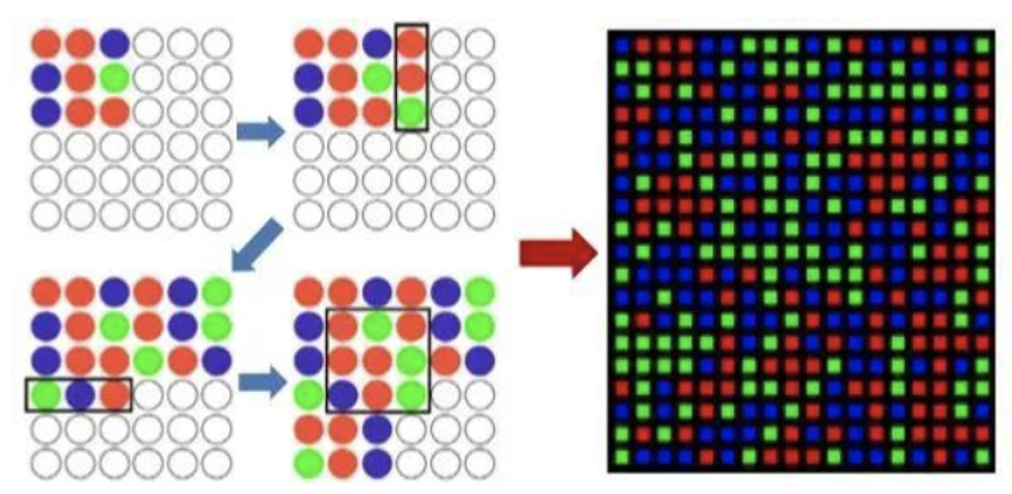
同样也可以利用RGB信息来进行二维编码,有相关算法来产生一些伪随机二维编码。如在下图中,左边展示了一个6*6大小的二维矩
阵,子窗口的大小为3*3。算法首先在左上角的3*3子窗口中随机填入各种颜色;然后一个3*1大小的滑动窗口移动到右端第一个空白处,并随机填入3中颜色;在填入生成的随机颜色前,算法会先验证子窗口的编码的唯一性能不能得到保证,若不能,则会重新生成3中随机颜色:如此循环,只是在竖直方向上滑动窗口的大小变为1*3,直至将整个6*6矩阵填满。下图则是该算法产生的某种伪随机二维编码的示例。
通讨以上对空间编码的讨论,也可以看出空间编码结构光的一些优缺点:
优点:
·无需多张照片,只需要一对影像即可进行三维重建Q。可以满足实时处理,用在动态环境中。
缺点
·易受噪声干扰:由于反光、照明等原因可能导致成像时部分区域等编码信息缺失;
·对于空间中的遮挡比较敏感:
·相较于时序编码结构光精度较低。








 投诉建议
投诉建议