设计仿真 | Adams 实现二维样条数据的线性插值

01概  述  

在实际工程应用中，往往能够通过试验等方式得到一定的离散数据，Adams软件使用样条函数或用户子程序对导入的离散数据进行插值以创建一个连续函数（也即曲线拟合），以方便工程师将试验数据应用到仿真分析中。

曲线拟合有样条函数或用户子程序两种实现方式，均有两种插值方法：Akima方法和传统立方插值方法。Akima方法（AKISPL函数）是局部三次拟合技术，传统立方插值方法（CUBSPL函数）是全局三次拟合技术，这两种方法都是通过使用三次多项式来实现曲线插值拟合。

除了曲线插值（非线性）拟合，实际工程中有时候也需要实现二维样条数据的线性插值，为了实现线性插值，一种变通的方法是将其转化为三维样条数据，当然另外一种方法是在局部位置增加点数，使拟合曲线的趋势接近线性插值，本文给出第一种方法的具体使用说明。

02线 性 插 值  

在进行线性插值的使用方法介绍之前，有必要了解下Adams软件曲线拟合技术背后的技术原理。Adams软件曲线拟合技术既支持二维样条数据，也支持三维样条数据，对于二维样条数据（只有一个独立的变量），Adams Solver（C++）使用三次多项式实现数据插值。对于三维样条数据（有两个独立的变量），先使用三次多项式插值方法在第一个独立变量的点之间插值，然后使用线性插值方法在第二个独立变量的曲线之间进行插值。

基于上述三维样条数据曲线拟合的技术原理，为了实现二维样条数据的线性插值，可以将二维样条数据导入后，对其进行简单的编辑，以转化为三维样条数据。具体实现方法如下：

1) 已知数据点（x,y）的一组数，x是第一个独立变量， y是非独立的变量。引入第二个独立变量z，即将Type由y=f(x) (2D)切换为y=f(x,z) (3D)。编辑数据z, 和第一个独立变量x的值相同，表格中y的值分别更改为Y1-1，Y2-1，Y3-1等，如下图 1所示。

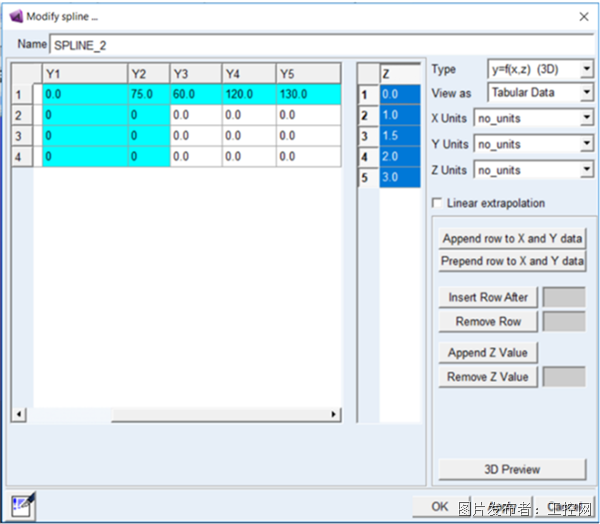
图 1  二维样条数据转化为三维样条数据的方式

2) 通过AKISPL函数对图1编辑好的三维样条数据进行线性插值，应用格式为：FUNCTION=AKISPL（0，time，SPLINE_1，0），这里使用第二个独立变量z，第一个独立变量x为0。

下面对AKISPL函数调用的格式进行补充说明，AKISPL函数调用格式为：AKISPL（x,z,id,iord），其中：

● x: 第一个独立变量；

● z: 第二个独立变量；

● id: 样条曲线的名称；

● iord: 插值点导数的阶次，属于整型变量，默认为0， 0≤iord≤2。

03应  用  

为了更清晰地理解如何在Adams软件中实现线性插值，下文给出一个简单的案例进行说明：

1) 已知二维数据（.txt）

0 0

1 75

1.5 60

2 120

3 130

2) 导入2D数据

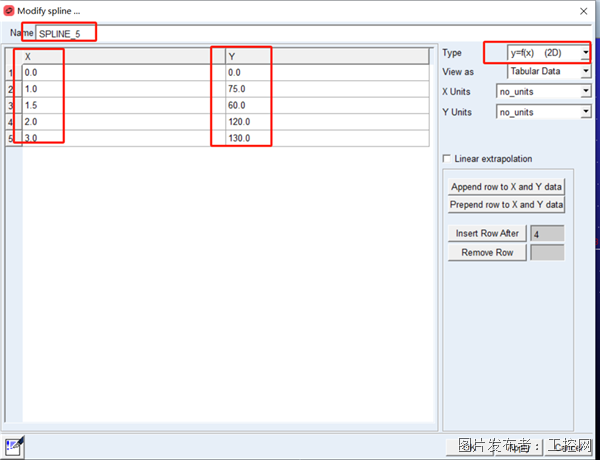
图 2  二维样条数据

3) 编辑2D数据

在Type类型中切换为y=f(x,z) (3D)，编辑Y和Z的数据，如下图 3所示。

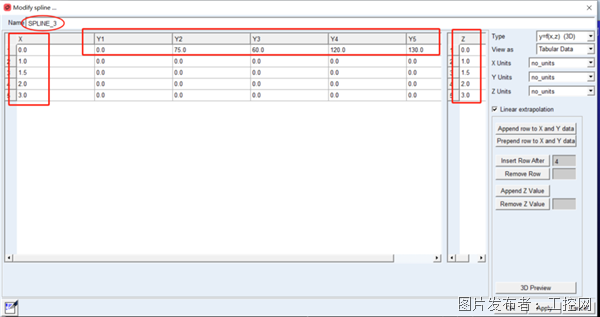
图 3  二维样条数据转为三维样条数据

4) 线性插值结果预览

编辑完样条数据后，可通过3D Prewiew对插值拟合曲线进行预览，如下图 4所示。

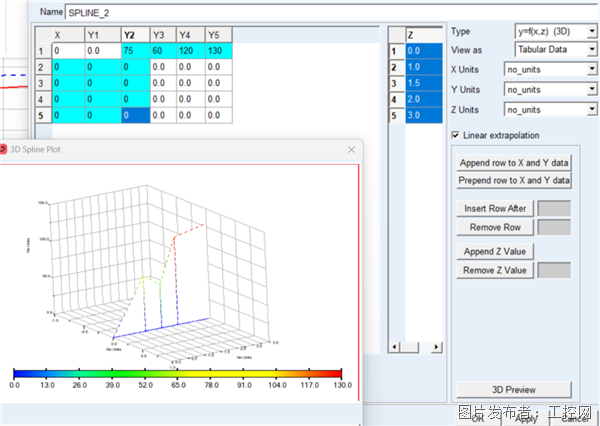
图 4   线性插值结果预览（3D Preview）

5) 通过函数实现线性插值

下面通过一个单点力函数表达式的建立验证线性插值的结果。

定义单点力，编辑AKISPL函数表达式，实现线性插值，如图 5所示。

● 第一个参数表示第一个独立变量，没有则设为0；

● 第二个参数表示第二个独立变量，设为time；

● 第三个参数表示样条曲线的名称；

● 第四个参数表示插值点导数的阶次（整数），设为0.

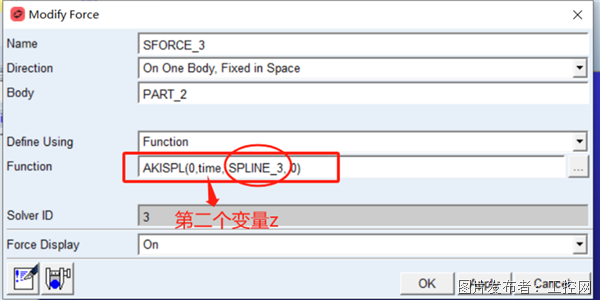
图 5  线性插值的设置（AKISPL函数）

6) 三次样条插值的函数设置

为了和线性插值的结果进行对比，下面给出了AKISPL函数和CUBSPL函数进行三次样条插值的设置。

定义一个单点力，定义函数表达式为AKISPL函数，实现三次样条插值，如图 6所示。

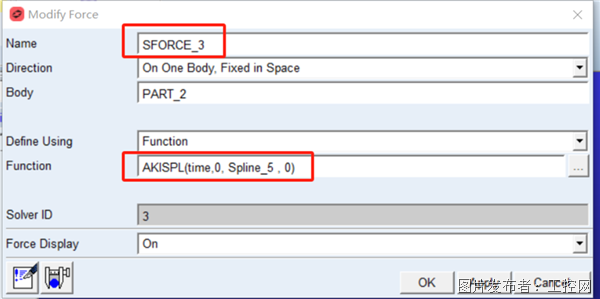
图 6  样条插值AKISPL函数的设置

定义一个单点力，定义函数表达式为CUBSPL函数，实现三次样条插值，如图 7所示。

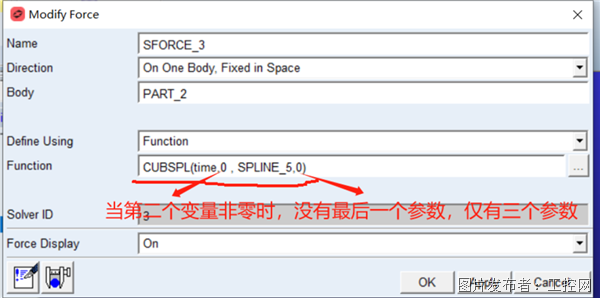
图 7  样条插值CUBSPL函数的设置

7) 三种插值结果的对比

定义测量，分别输出三种插值的结果曲线如下图 8所示。

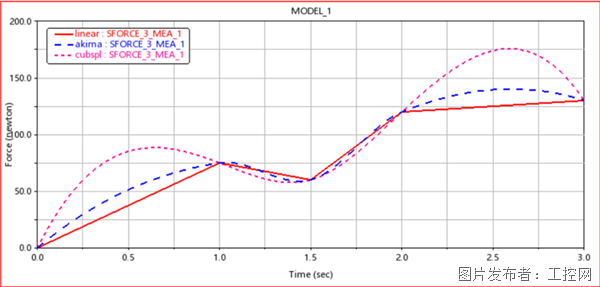
图 8  线性插值和三次样条插值结果对比

04总  结  

为了实现二维样条数据的线性插值，可以通过样条曲线的方式，只是需要在样条曲线的基础上做一点变通。本文中函数调用的方式给出的自变量是时间，实际应用中自变量也可以是其它变量，比如频率或其它，可以先通过函数进行定义，然后选择定义的变量名称作为自变量即可。